Quantum Field Theory (QFT) is a unified language, a toolbox, a set of techniques for modern theoretical physicists. And it has had tremendous success with it’s, in my eyes, brightest achievement being the standard model of particle physics, but also the explanation of superconductivity, Hall effect and others. Important things!
So what is it?
First, we have to go through some words again.
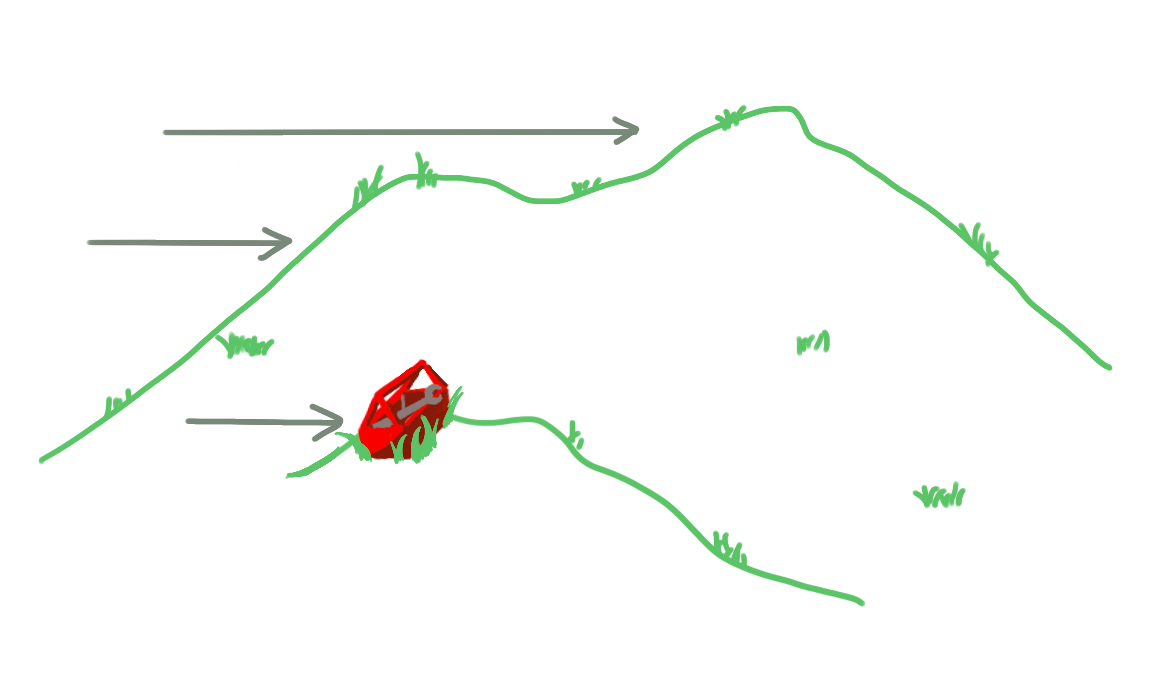
What is a field? Imagine a hilly landscape with a coordinate grid beneath it. The ‘field’ in this case could be the height of each point above the ground (i.e. a number). An arrow (a vector, really) at each point pointing in the wind’s direction would also be a field. More abstractly speaking, a field assigns to each point in space (and possibly time) a value, like a number, vector or something else.
A QFT now just naturally incorporates quantum fluctuations and, thus, describes quantum fields.
An absurdly short attempt to explain quantum fluctuations (stay tuned for a possible post on quantum mechanics): Due to nature’s inherent property of uncertainty, i.e. the inability to determine the position and velocity of a particle with perfect precision, this uncertainty carries over to our field of the QFT. So we call this ‘uncertainty’ a quantum fluctuation, as it randomly changes the content, like the height or arrow, of the field. You can really imagine it as a hilly landscape that randomly fluctuates, but only on a very small scale.
Regarding the particles we are comprised of. The key to QFT is to treat particles as if they were excitations of quantum fields (read: “peaks in the landscape”). The mathematics underlying this proclamation are a bit dry, so let us jump to the technique by which physicists try to describe nature using wobbly fields: path integrals.
Path integrals are a real nightmare for mathematicians and as of today, I am not sure ‘why’ they work at all, but they do.
Imagine a double slit experiment. A particle, two passable slits, and a detector on the other side. A classical particle (like a tennis ball) passes through either slit. A quantum particle however interferes with itself and leaves a nice interference pattern.
Richard Feynman asked what would happen if we considered all possible paths the particle could go, yes all. And then add the paths in a weighted average. This idea was simply revolutionary.
Carrying out the maths, one makes some observations:
- The weight of the paths entirely determines the physics.
- The weight is really big for paths which are classical (straight to the detector in the double slit experiment) or nearly classical (like small deviations from a straight line).
- The weight is really small for unreasonable paths (like around the world and into the detector).
Effectively, the situation often looks like this: We can describe a system with good approximation as classical systems with small quantum fluctuations. This is why QFT is the perfect formalism for this.
Over the years, many methods have been introduced to tackle several problems. Quantum gauge theory, from my last article, being one of them, and Perturbation theory using Feynman diagrams, a neat mnemonic method, being another one.
QFT has proven to predict very precise results, especially in the regime of elementary particles. However it is ridden with many problems, like the (in many cases) questionable mathematical foundation and the appearance of infinities. Some believe this is due to the fact QFTs only describe a portion of reality with good precision, but are really part of an overarching theory, which does not suffer from these problems.

One reply on “What is Quantum Field Theory?”
Recap: There are quantum fluctuations, which affect everything all the time. They can be described as fields… and added on top of classical fields? Turning a classical landscape into a wobbly landscape? Because fluctuations are different from quantum excitations, right? That’s where particles come into play? So I am a wobbly excited peak in the spacetime of quantumthings? Or are excitations and fluctuations the same? Surely not, because then everything would be a homogeneous quantum soup…